
Recommender systems are a vital tool in a data scientists’ toolbox. The aim is simple, given data on customers and items they’ve bought, automatically make recommendations of other products they’d like. You can see these systems in action on a lot of websites (for example Amazon), and it’s not just limited to physical products, they can be used for any customer interaction. Recommender systems were introduced in a previous Cambridge Spark tutorial.
In this tutorial, we want to extend the previous article by showing you how to build recommender systems in python using cutting-edge algorithms. Many traditional methods for training recommender systems are bad at making predictions due to a process known as overfitting. Overfitting in the context of recommender systems means our model will be good at fitting to the data we have, but bad at recommending new products to customers (not ideal given that is their purpose). This is because there is so much missing information. Before getting into the code, we’ll give more details about recommender systems, why there is so much missing information, and its solution.
Recommender Systems and Matrix Factorisation
The data input for a recommender system can be thought of as a large matrix, with the rows indicating an entry for a customer, and the columns indicating an entry for a particular item. Let’s call this matrix . Then entry will contain the score that customer has given to product . For example if it’s a review this could be a number from 1–5, or it might just be 0–1 indicating if a user has bought an item or not. This matrix contains a lot of missing information, it’s unlikely a customer has bought every item on Amazon! Recommender systems aim to fill in this missing information, by predicting the customer score of items where the score is missing. Then recommender systems will recommend items to the customer that have the highest score. A typical example of the matrix with entries that are review values from 1–5 is given in the picture below.
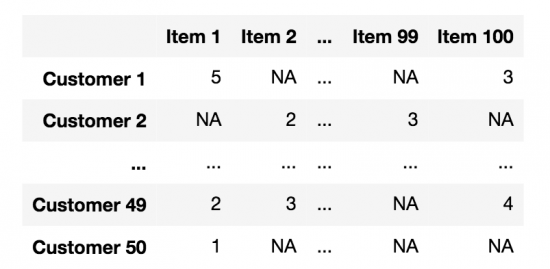
The Netflix challenge was a competition designed to find the best algorithms for recommender systems. It was run by Netflix using their movie data. During the challenge, one type of algorithm stood out for its excellent performance, and has remained popular ever since. It is known as matrix factorisation. This method works by trying to factorise the matrix into two lower dimensional matrices and , so that =ᵀ.
Suppose that R has dimension ₁×₂, then U will have dimension ×₁ and V will have dimension ×₂. Here is chosen by the user, it needs to be large enough to encode the nuances of , but making it too large will make performance slow and could lead to overfitting. A typical size of is 20.
While at first glance, this factorisation seems quite easy, it is made much more difficult by all the missing data. Imputing the data might work, but it makes the methods very slow. Instead, most popular methods focus only on the matrix entries that are known, and fit the factorisation to minimise the error of these known . A problem with doing this though is that predictions will be bad because of overfitting. The methods get around this by using a procedure known as regularisation, which is a common way to reduce overfitting. For more details about the workings of the methods, please see the further reading at the end of this post.
The Package
In this tutorial, we’ll use the surprise package, a popular package for building recommendation systems in Python. Mac and Linux users can install this package by opening a terminal and running pip install surprise. Windows users can install it using conda conda install -c conda-forge scikit-surprise. The package can then be imported in the standard way,

The Dataset
In this tutorial, we’ll work with the librec FilmTrust dataset, originally collated for a particular recommender systems paper. The dataset contains 35497 movie ratings from various users of the FilmTrust platform. We chose this dataset as it is relatively small, so examples should run quite quickly. The package surprise has a number of datasets built in, but we chose this one as it allows us to demonstrate how to load custom datasets into the package. Normally, recommender systems will use larger datasets than this, so for more challenging datasets we recommend investigating the grouplens website, which has a variety of free datasets available.
First we’ll download the dataset from the web and load in the data file as a pandas dataframe. We can do this using the following commands:
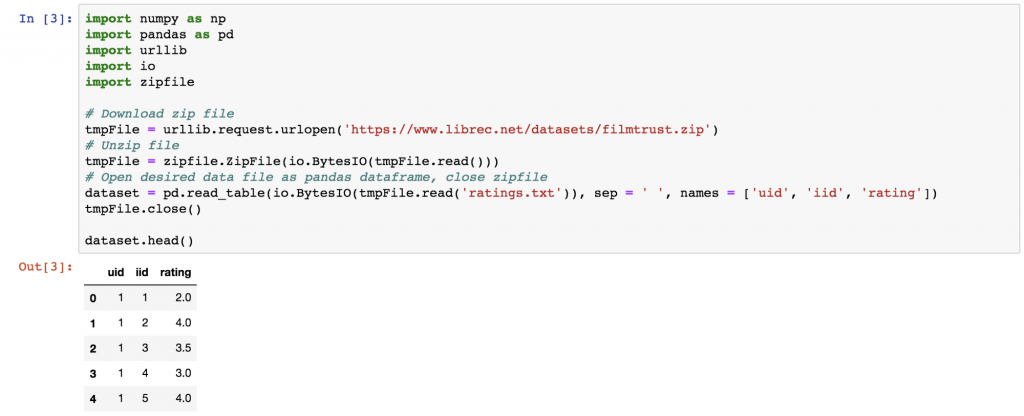
As you can see this dataset does not really look like the matrix RR. This is because there are so many missing values, so it is much easier to save the file in a sparse format. In a sparse format, the first column is the row number of the matrix ii; the second column is the column number of the matrix jj; and the third row is the matrix entry RijRij. For this dataset, the first column is the user ID, the second is the ID of the movie they’ve reviewed, and the third column is their review score. This sparse format is also the input that matrix factorisation methods require, rather than the full matrix RR, this is because they only use the non-missing matrix entries.
Fitting the Model
Now it’s time to start using the package. First we need to load the dataset into the package surprise, this is done using the Reader class. The main thing the Reader class does is to specify the range of the reviews. Let's first check the range of the reviews for this dataset.

So our review range goes from 0.5 to 4, which is a little non-standard (the default for surprise is 1-5). So we will need to change this when we load in our dataset, which is done like this:

We will use the method SVD++, one of best performers in the Netflix challenge, which has now become a popular method for fitting recommender systems. As we mentioned earlier, this method extends vanilla SVD algorithms such as the one covered in the previous blog post by only optimising known terms and performing regularisation (note that the method SVD in surprise is much more sophisticated than vanilla SVD, and much more similar to SVD++). More details on method specifics can be found in the further reading. A simple recommender system built with the SVD++ can be coded as follows:

For now we’ve just trained the model on the whole dataset, which is not good practice but we do it just to give you an idea of how the models and predictions work. Later on we’ll cover proper testing and evaluation; as well as hyperparameter tuning to maximise performance.
Now we’ve fitted the model, we can check the predicted score of, for example, user 50 on a music artist 52 using the predict method.

So in this case the estimate was a score of 3. But in order to recommend the best products to users, we need to find n items that have the highest predicted score. We'll do this in the next section.
Making Recommendations
Let’s make our recommendations to a particular user. Let’s focus on uid 50 and find one item to recommend them. First we need to find the movie ids that user 50 didn’t rate, since we don’t want to recommend them a movie they’ve already watched!

Next we want to predict the score of each of the movie ids that user 50 didn’t rate, and find the best one. For this we have to create another dataset with the iids we want to predict in the sparse format as before of: uid, iid, rating. We'll just arbitrarily set all the ratings of this test set to 4, as they are not needed. Let's do this, then output the first prediction.

As you can see from the output, each prediction is a special object. In order to find the best, we’ll convert this object into an array of the predicted ratings. We’ll then use this to find the iid with the best predicted rating.

When you implement your own recommender system you will normally have metadata which allows you to get, for example the name of the film from the iid code. Unfortunately, this dataset does not include this information, but many other larger datasets do, such as the movielens dataset.
Similarly you can get the top n items for user 50, just replace the argmax()method with the argpartition() method as per this stackoverflow question.
Tuning and Evaluating the Model
As you probably already know, it is bad practice to fit a model on the whole dataset without checking its performance and tuning parameters which affect the fit. So for the remainder of the tutorial we’ll show you how to tune the parameters of SVD++ and evaluate the performance of the method. The method SVD++, as well as most other matrix factorisation algorithms, will depend on a number of main tuning constants: the dimension DD affecting the size of UU and VV; the learning rate, which affects the performance of the optimisation step; the regularisation term affecting the overfitting of the model; and the number of epochs, which determines how many iterations of optimisation are used.
In this tutorial we’ll tune the learning rate and the regularisation term. SVD++has more than one learning rate and regularisation term. But surprise lets a fixed value be set for all the learning rate values, and another for all the regularisation terms, so we'll do this for speed. In surprise, tuning is performed using a function called GridSearchCV, which picks the constants which perform the best at predicting a held out testset. This means constant values to try need to be predefined.
First let’s define our list of constant values to check, typically the learning rate is a small value between 0 and 1. In theory, the regularisation parameter can be any positive real value, but in practice it is limited as setting it too small will result in overfitting, while setting it too large will result in poor performance; so trying a list of reasonable values should be fine. The GridSearchCV function can then be used to determine the best performing parameter values using cross validation. We've chosen quite a limited list since this code can take a while to run, as it has to fit multiple models with different parameters.

The output prints the combination of parameters that gets the best RMSE on a held out test set, RMSE is a way of measuring the prediction error. In this case, we’ve only checked a few tuning constant values, because these procedures can take a while to run. But typically you will try out as many values as possible to get the best performance you can.
The performance of a particular model you’ve chosen can be evaluated using cross validation. This might be used to compare a number of methods for example, or just to check your method is performing reasonably. This can be done by running the following:

Further Reading
Now you know how to fit high performing recommender systems using the Python package surprise, as well as using this to generate predictions for users, and how to tune your system for maximum performance. I recommend checking out the documentation for surprise to help really get to grips with the package, maybe play around with the tuning constants to get to know how to maximise performance of your recommendation system, as well as trying the package out with more complicated or larger datasets.
For those that want to know more, outlined here is some recommended reading:
- Get the top 10 scoring items for each user: package FAQ for
surprise - Review paper of matrix factorisation methods for recommender systems
- Repository of matrix factorisation datasets at Grouplens
- Another article on matrix factorisation which has more detail on the underlying maths

About the author
Jack Baker is a statistics student, undertaking his PhD at the University of Lancaster, in collaboration with the University of Washington.
-1.png)
Enquire now
Fill out the following form and we’ll contact you within one business day to discuss and answer any questions you have about the programme. We look forward to speaking with you.
